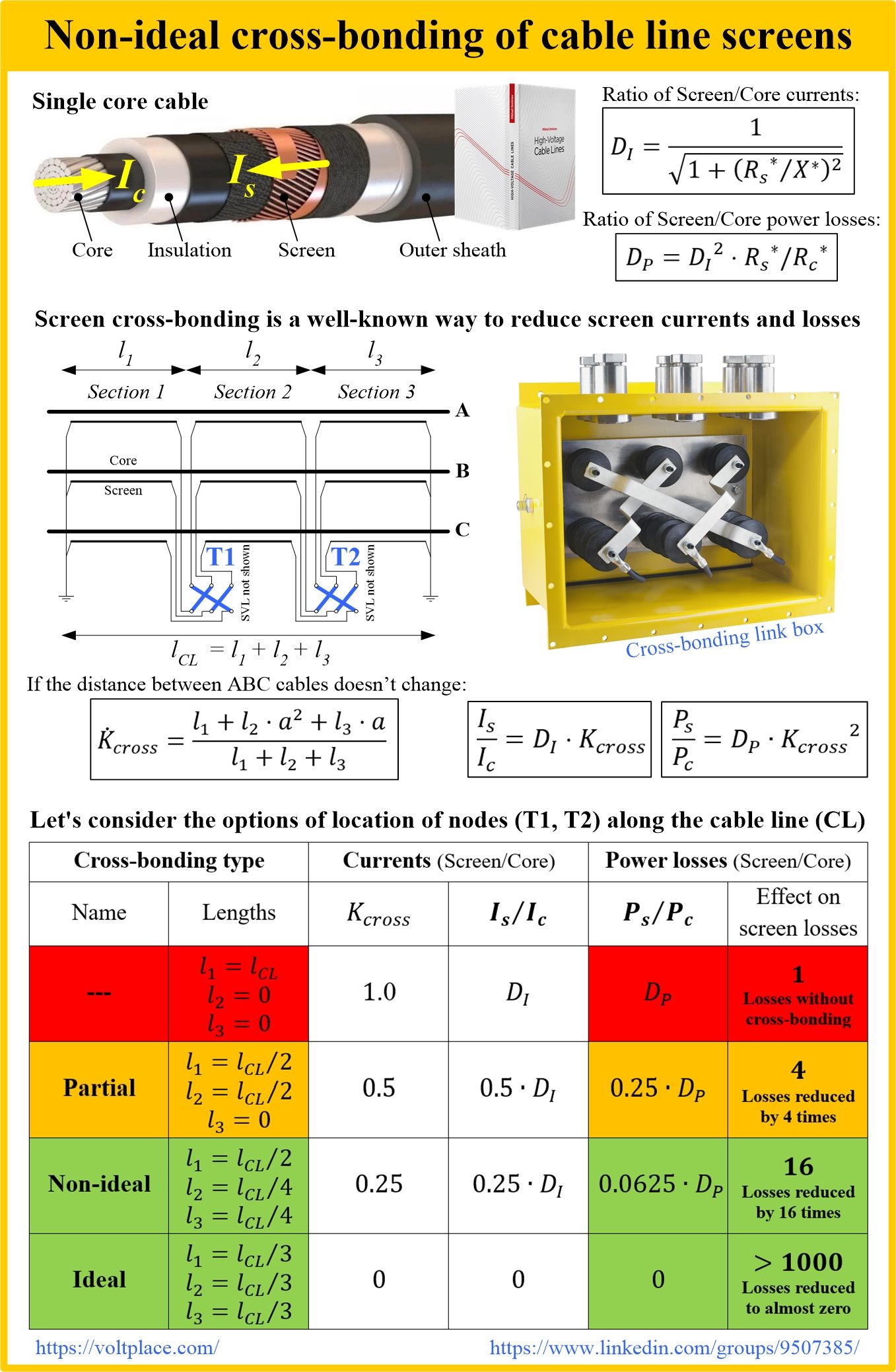
Non-ideal screen cross-bonding
Single-core cables are used in networks of all voltage classes from 6 to 500 kV. Such cables have conductive screens (CU or AL), and these screens are often grounded on both sides. This leads to the appearance of significant longitudinal induced currents (Is) in the screens caused by the 50 Hz magnetic field of the core currents (Ic). In turn, currents in the screens cause losses in the screens (Ps), which can be up to 3-4 times greater than the losses in the cores (Pc).
There are many different ways to reduce currents in screens, including laying phases ABC in a closed triangle and using cables with a small screen cross-section. If these measures are not possible for one reason or another, then it is necessary to abandon the simple two-side grounding of the screens in favor of one of the alternative schemes:
✅ one-side grounding of screens (for “short” cable lines);
✅ cross-bonding of screens.
The screens cross-bonding (let’s say we’re talking about one full cycle today) assumes that we divide the cable line (CL) route into three sections (1,2,3), and put cross-bonding joints and link boxes at their junctions.
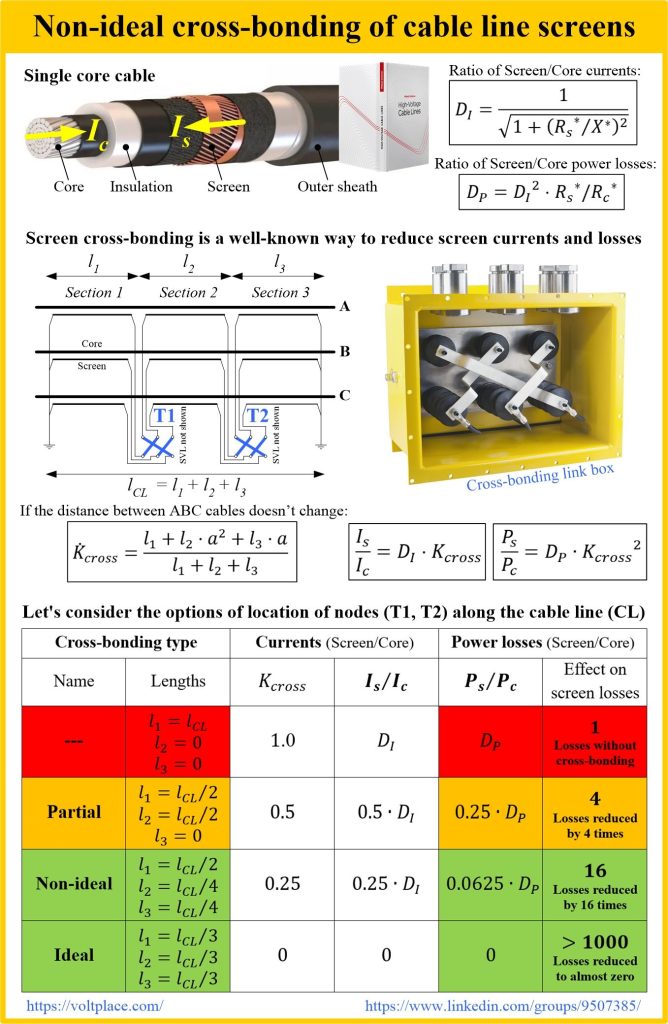
Looking at the design experience, I must say that designers go crazy trying to maintain the L1=L2=L3 rule. My post is that it’s useless for two reasons:
1️⃣ The mutual arrangement of the ABC cables varies along the route (somewhere in a row, somewhere in a triangle, somewhere in the pipes), and therefore even L1=L2=L3 does not provide zero currents in the screens.
2️⃣ If we assume that the mutual arrangement does not change (the distances between the phases are the same, S1=S2=S3), then our task is not to ensure zero currents and losses in the screens, but at least to reduce them compared to the case of a simple two-side grounding of the screens.
Please look at the table with the results of calculations:
✅ Even partial cross-bonding (one box divides the CL in half), we already have a 4-fold reduction in screen losses compared to the case without cross-bonding at all.
✅ Even a non-ideal cross-bonding (the considered case: the length L1 is twice as long as the length of the L2 and L3) we already have a 16-fold reduction in screen losses compared to the case without cross-bonding at all.
There is no point in aiming for L1=L2=L3. Even a serious difference in the lengths of L1, L2, and L3 will still give you a tenfold reduction in screen losses compared to the case without cross-bonding at all.
The inability to provide L1=L2=L3 cannot in any case be a reason for rejecting the cross-bonding of screens.
Item 4.2.3 of the book contains simple and precise formulae that will allow you to evaluate the effectiveness of screen cross-bonding, taking into account differences:
1️⃣ in the distance between the ABC phases in three sections (S1, S2, S3).
2️⃣ in the length of three sections (L1, L2, L3).
